本系列文章部分內容由AI產生，最後皆有通過人工確認內容及潤稿。

在前兩天的學習中，我們了解了人工智能（AI）、機器學習（ML）和深度學習（DL）的基本概念，以及深度學習中的一些重要組成部分。今天，我們將深入探討神經網絡的基礎，特別是感知器和多層感知器（MLP）的原理，以及激活函數和損失函數在神經網絡中的作用。

本日學習目標

理解感知器的基本原理
掌握多層感知器的結構和工作方式
了解激活函數和損失函數在神經網絡中的作用
能夠手動計算簡單神經網絡的輸出

感知器（Perceptron）

感知器的起源

感知器是最基本的人工神經網絡模型，由Frank Rosenblatt在1957年提出。它是模仿生物神經元的計算模型，用於二分類任務。

感知器的結構

一個感知器包括以下部分：

• 輸入（Inputs）：X1, X2,...Xn
• 權重（Weights）：W1, W2,...Wx
• 偏置（Bias）：b
• 激活函數（Activation Function）：f

感知器的工作原理

感知器的輸出計算如下：

• 線性組合：
  
• 激活函數：
  
• 常用的激活函數在感知器中通常是階躍函數（Step Function）：
  

感知器的應用與局限

• 應用：感知器可以用於線性可分的二分類問題。
• 局限：感知器無法解決非線性問題，例如異或（XOR）問題。
  
  圖1 感知器的結構圖，包含輸入、權重、偏置和激活函數。

多層感知器（MLP）

為何需要多層感知器

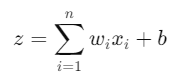
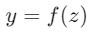
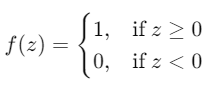
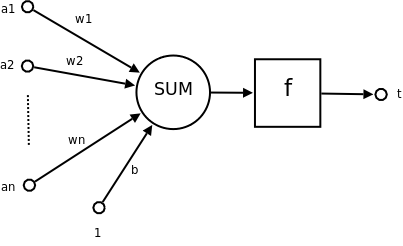
由於單個感知器無法解決非線性可分問題，引入多層感知器以提高模型的表現力。

多層感知器的結構

• 輸入層（Input Layer）： 接收原始數據。
• 隱藏層（Hidden Layers）： 一個或多個，負責特徵提取和非線性變換。
• 輸出層（Output Layer）： 產生最終預測結果。

前向傳播（Forward Propagation）

在MLP中，數據從輸入層經過隱藏層傳遞到輸出層，每一層的輸出成為下一層的輸入。
對於第𝑙層的神經元，其輸入和輸出計算為：

1. 線性組合：

• W：第𝑙層的權重矩陣
• a：第(𝑙−1)層的激活值
• b：第𝑙層的偏置向量

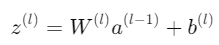
由於這邊不好打上下標，所以就以英文字母為代表

2. 激活函數：

非線性激活函數的重要性

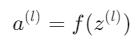
引入非線性激活函數，使得神經網絡可以擬合非線性關係。如果沒有非線性激活函數，無論網絡多深，輸出都是輸入的線性組合。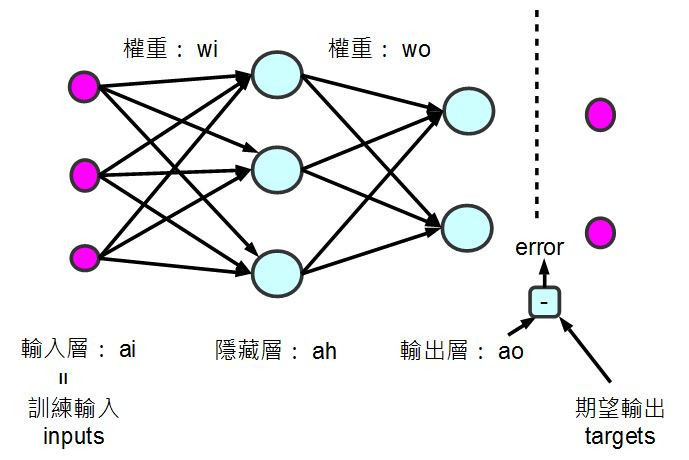

圖2 多層感知器包含輸入層、隱藏層和輸出層。

激活函數（Activation Functions）

激活函數的部份我們昨天有提過，所以今天我們就簡單地複習帶過

常見的激活函數：

• Sigmoid函數
• Tanh函數
• ReLU（Rectified Linear Unit）
• Leaky ReLU
• ELU（Exponential Linear Unit）
• Maxout

常見激活函數的選擇

• 隱藏層：通常使用ReLU及其變體（如Leaky ReLU、ELU）。
• 輸出層：
  • 二分類問題： Sigmoid 函數。
  • 多分類問題： Softmax 函數。
  • 回歸問題： 線性激活函數或ReLU。

一定要記住！！選擇沒有絕對，可以嘗試看看以最適合自己的模型為主

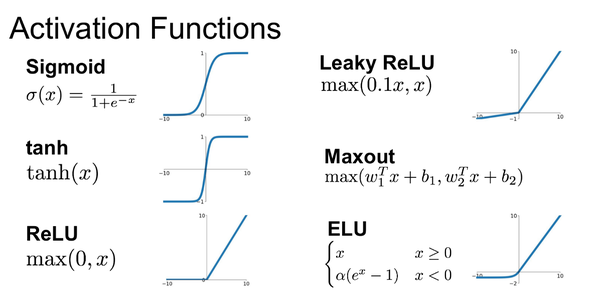
圖3 常見激活函數曲線

損失函數（Loss Functions）

損失函數的作用

損失函數衡量模型預測值與真實值之間的差異，是訓練神經網絡的核心。通過最小化損失函數，模型可以學習到更準確的權重。

常見的損失函數

• 均方誤差（Mean Squared Error, MSE）：常用於回歸問題。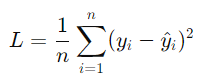
  

• 交叉熵損失（Cross-Entropy Loss）：常用於分類問題。

  • 二分類交叉熵：
    
  • 多分類交叉熵：
    

  損失函數的選擇

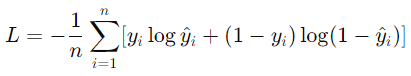
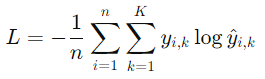
• 回歸問題： 使用MSE或MAE（平均絕對誤差）。

• 分類問題： 使用交叉熵損失。

神經網絡的訓練

前向傳播（Forward Propagation）

將輸入數據經過網絡，計算輸出和損失。

反向傳播（Backward Propagation）

計算損失對各層權重的梯度，使用鏈式法則。

• 鏈式法則：
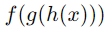  對於複合函數 ，其導數為：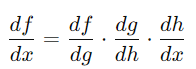

更新權重

使用優化算法（如梯度下降）更新權重：

• 梯度下降法：
  
  • η：學習率

優化算法

• 批量梯度下降（Batch Gradient Descent）
• 隨機梯度下降（Stochastic Gradient Descent, SGD）
• 小批量梯度下降（Mini-batch Gradient Descent）
• 自適應學習率方法： 如Adam、RMSprop、Adagrad

手動計算簡單神經網絡的輸出

示例

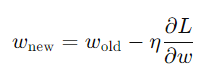
考慮一個簡單的單隱藏層神經網絡：

• 輸入層： 2個神經元
• 隱藏層： 2個神經元，使用ReLU激活函數
• 輸出層： 1個神經元，使用Sigmoid激活函數

給定參數

• 輸入：
  
  • 權重和偏置：
    隱藏層權重矩陣W1：
    
  • 隱藏層偏置：
    
  • 輸出層權重向量W2：
    
  • 輸出層偏置b2=0

計算過程

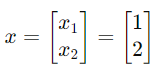
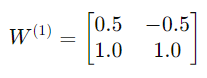
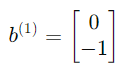
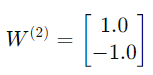
Step 1：計算隱藏層輸入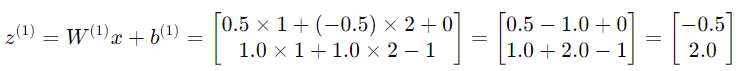

Step 2：計算隱藏層輸出
使用ReLU激活函數：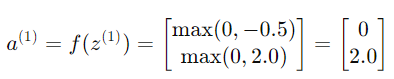
Step 3：計算輸出層輸入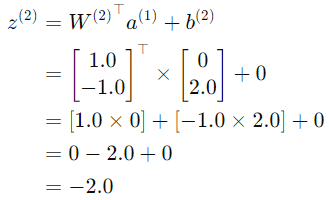

Step 4：計算輸出層輸出
使用Sigmoid激活函數：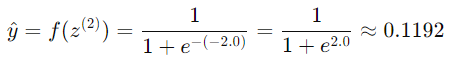

總結

今天學習，雖然計算與微積分內容很多，但我們深入了解了神經網絡的基礎知識，從感知器到多層感知器，並掌握了激活函數和損失函數在神經網絡中的作用。我們還親手計算了一個簡單神經網絡的輸出，加深了對神經網絡工作原理的理解。
那我們明天見！

推薦資源

• Neural Networks Demystified [Part 2: Forward Propagation]

參考資源

圖1 來源 神經網路
圖2 來源 多層感知器與反傳遞演算法實作-使用 JavaScript+Node.js
圖3 來源 Introduction to Exponential Linear Unit